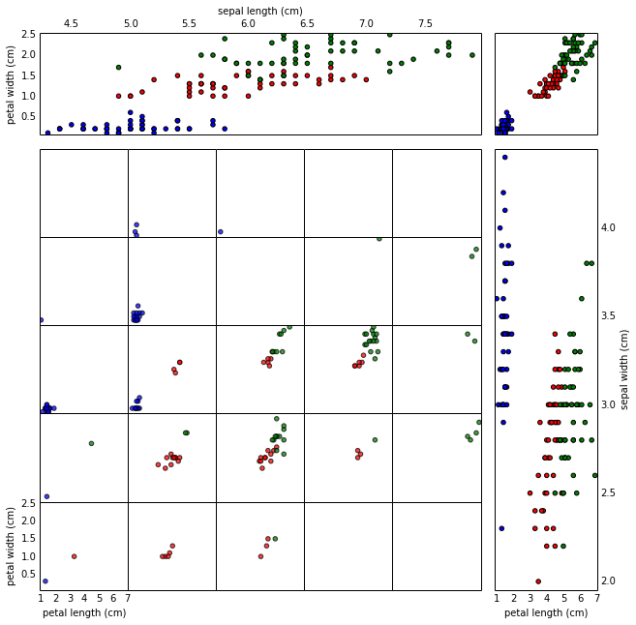
I recently had the pleasure of reading James Scott’s “Seeing Like a State,” which examines a certain strain of failure in large centrally-organized projects. These failures come down to the kinds of knowledge available to administrators and governments: aggregates and statistics, as opposed to the kinds of direct experience available to the people living ‘on the ground,’ in situations where the centralized knowledge either fails to or has no chance to describe a complex reality. The book classifies these two different kinds of knowledge as techne (general knowledge) and metis (local knowledge). In my reading, the techne – in both strengths and shortcomings – bears similarity to the knowledge we obtain from traditional algorithms, while metis knowledge is just starting to become available via statistical learning algorithms.
In this (kinda long) post, I will outline some of the major points of Scott’s arguments, and look at how they relate to modern machine learning. In particular, the divides Scott observes between the knowledge of administrators and the knowledge of communities suggest an array of topics for research. Beyond simply looking at the difference between the ways that humans and machines process data, we observe areas where traditional, centralized data analysis has systematically failed. And from these failures, we glean suggestions of where we need to improve machine learning systems to be able to solve the underlying problems.