Stable Diffusion is the best neural text-to-image engine you can run on your own hardware. I recently picked up a new 3090 for my home machine, and spent a couple weekends messing around with Stable Diffusion. Initially, I’ve been using it to generate concept art for a game of Apocalypse World, a tabletop roleplaying game. Stable Diffusion really shines in this space; the creation of the concept art becomes a bit of a collaborative dance, as I find new ideas in the ML output that might get incorporated into the game. The rich imagery also helps create a shared universe for the players, not too unlike the incredibly rich art that TTRPG books tend to invest in. And the small scale of a single TTRPG game, with just a few players, means that we can add concept art to a place where it never would have existed before. These kinds of ML tools are fantastic for lowest-rent collaborative creative exercises.

Having full access to the model + execution code makes it really straightforward to get into the guts and start tinkering with non-standard use cases. I was particularly interested in mucking around with the various latent/hidden representations used by the model. In this post, I’ll a) explain the parts of the model (briefly), then explain how I b) used the text embedding latents to create some simple animations and c) to sample lots of minor variations of an image.

Model overview

To get started, it’s quite easy to copy the ‘Writing your own inference pipeline‘ section of the Stable Diffusion docs on HuggingFace. Copy out the process, and then check that the code actually runs and produces images.

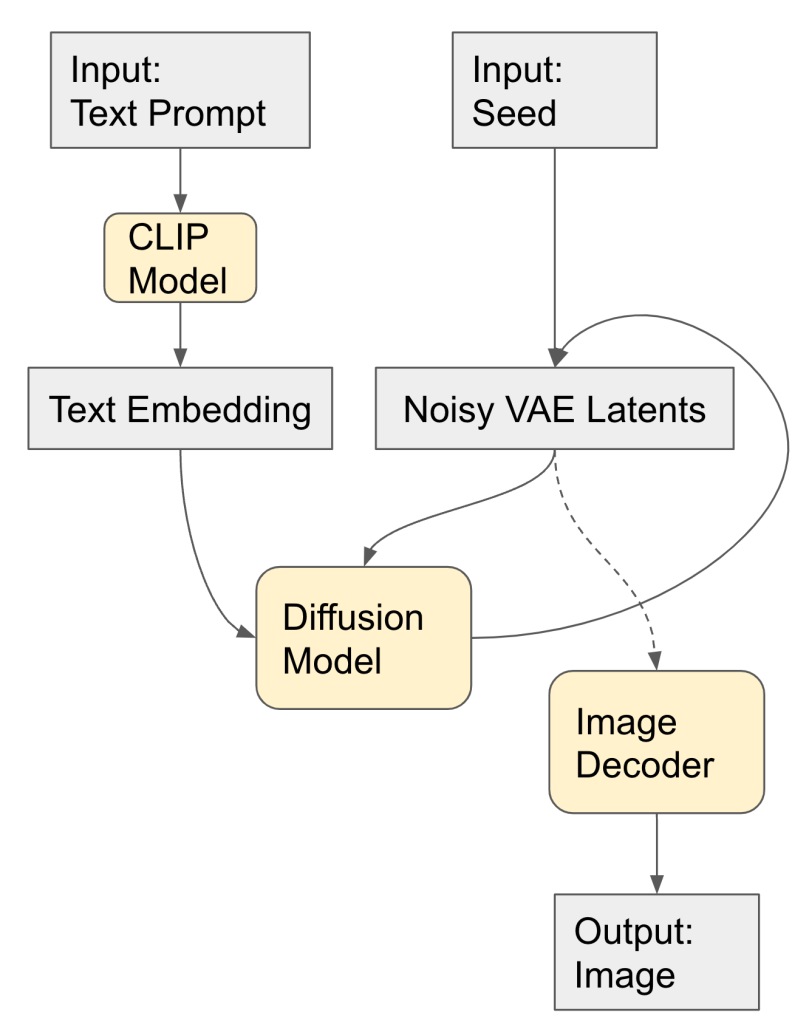
To start mucking around with the latents, it helps to have a good understanding of the model structure.

1. The model takes as inputs a text prompt and a random seed.
2. These are used to create a text embedding and initial pure-noise VAE latents.
3. The diffusion algorithm progressively de-noises the VAE latents to obtain a ‘clean’ latent image which matches the text prompt to some extent. (As an aside, at each step new noise is generated and added to the de-noised image; you really need to use the same random generator seed, and not just the same initial noisy VAE latent.)
4. The VAE decoder (very quickly) converts the de-noised latent image to a full sized output image.

So, if you run the same text prompt from the same random seed, you get the same image. Now, it turns out that a small change in the text embedding space mostly corresponds to a small change in the output image. This continuity makes the text embedding space a good playground.

Note that the VAE image latents are actually a pretty boring space, by comparison: the latents have shape [4, 64, 64] where the last dimensions correspond to image height and width. This blog post shows that the VAE latents are actually quite close to the image already. You can get some kind of effects by manipulating the VAE latents (for example, sending x to -x takes the color negative of the image more or less), but these effects aren’t terribly interesting, like degraded versions of what you’d try to do in Photoshop.

Morph Animations

Often you can make relatively small changes in the prompt and (so long as you use the same seed) you’ll bet back a very similar image, with some changes in the details. Then you can make a morph animation by ‘walking’ from one text embedding to the other, generating new images along the way. In the image morph animation, I’ve changed the famous actress’ name only, leaving the rest of the prompt the same, and connected the two with 16 transition frames.

Stable Diffusion isn’t great at making random faces (you tend to get mosnters), but tends to get the details /mostly/ right for famous people who show up in the dataset a lot. So, to get a good face, pick a famous name. The text embedding transformation gives a nice way to deal with the casual-deepfake problem, though: most of the ‘intermediate’ faces are still good, so we can create text embeddings for a couple-few people, interpolate, and then choose one which doesn’t look too much like any of the ‘source’ faces.

Here’s another example, interpolating between an abandoned street in a city vs a forest. The basic composition remains the same in both images, but one is full of buildings and neon, and the other is full of trees.

Generating Variations

Another neat application of continuity in the text embedding space is that you can use it to explore closely-related images and try to find something sliiightly better than the initial output. You can add noise repeatedly to the base text embedding to get lots of variants, in other words.

For this image, I added Gaussian noise to the text prompt with standard deviation 0.02 repeatedly. This was structured as a random walk: each new embedding y[k] = 0.5 * y[0] + 0.5 * (y[k-1] + noise). This can potentially create a nice animation over a longer random walk, as we have some coherency between adjacent steps. The first term (0.5*y[0]) ensures that we stay in the neighborhood of the original image.