technical – Inventing Situations.

Fibonacci Coding: for Fun, if not Profit.

July 3, 2021July 3, 2021sdenton4

Suppose we want to send a message to a friend using as few bits as possible… And let’s also suppose that this message consists of unit-normally-distributed real numbers. Now, it turns out that it’s really really expensive to send arbitrary precision real numbers: You could find yourself sending some not-previously-known-to-man transcendental number, and just have to keep listing off digits forever. So, in reality, we allow some amount of noise tolerance in the encoding.

This is a good problem to sink some effort into: Lots of data is roughly normally distributed, and if you’re sending some machine learned representation, you can introduce some regularization to ensure that the data is close to unit-normal. (This is, for example, the whole idea behind Variational Auto Encoders.)

I’ll start with a quick outline of a standard solution, and then we’ll go into a half-baked idea involving Fibonacci codes and space filling curves.

The basic idea comes in two parts:

First, Fibonacci coding lets you encode an arbitrarily large integer, without having to send the length of the integer before hand. (There’s a bunch of similar schemes you can use here, but the Fibs are fun and interesting.)
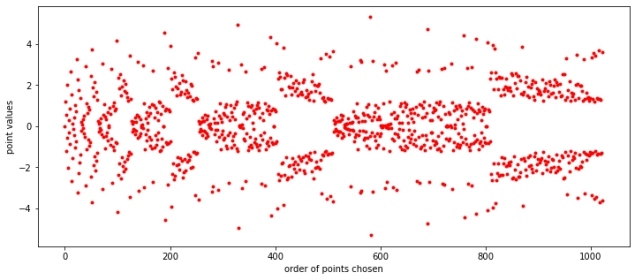
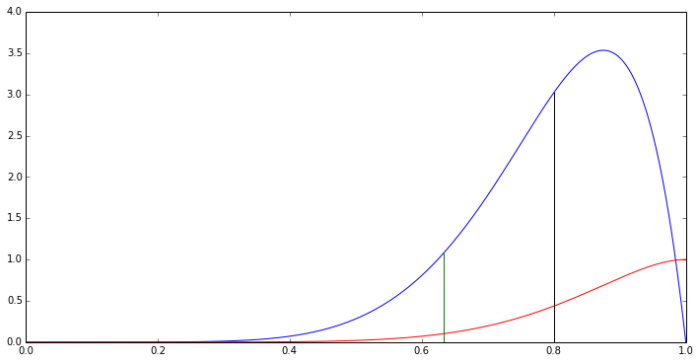
Second, map the integers into the reals in a way that covers the normal distribution in a ‘progressive’ way, so that we can use small numbers if we don’t need high precision, and only use bigger numbers as we need more precision.

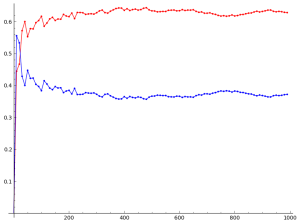
At the end we’ll run a few empirical tests and see how well the scheme works, and point to where there’s room for improvement.

Continue reading →

Evaluating Success Rates with the Beta Distribution

January 15, 2017January 17, 2017sdenton42 Comments

Suppose you’re building a widget that performs some simple action, which ends in either success or failure. You decide it needs to succeed 75% of the time before you’re willing to release it. You run ten tests, and see that it succeeds exactly 8 times. So you ask yourself, is that really good enough? Do you believe the test results? If you ran the test one more time, and it failed, you would have only an 72.7% success rate, after all.

So when do you have enough data, and how do you make the decision that your success rate is ‘good enough?’ In this post, we’ll look at how the Beta distribution helps us answer this question. First, we’ll get some intuition for the Beta distribution, and then discuss why it’s the right distribution for the problem.

The Basic Problem

Consider the widget’s tests as independent boolean variables, governed by some hidden parameter μ, so that the test succeeds with probability μ. Our job, then, is to estimate this parameter: We want a model for P(μ=x | s, f ), the probability distribution of μ, conditioned on our observations of success and failure. This is a continuous probability distribution, with μ a number between zero and one. (This general setup, by the by, is called ‘parameter estimation‘ in the stats literature, as we’re trying to estimate the parameters of a well-known distribution.)

beta8-2 — Beta distribution for 8 successes and 2 failures. The blue curve is the probability density function P(x=μ|s, f). The expected value for μ is 0.8 (marked in black). The green line indicates 90% certainty that mu is greater than 0.633. The red curve is the cumulative density function, which is useful for finding confidence bounds.

Continue reading →

Kaggle Social Networks Competition

November 9, 2014November 10, 2014sdenton4

This week I was surprised to learn that I won the Kaggle Social Networks competition!

This was a bit different from other Kaggle competitions. Typically, a Kaggle competition will provide a large set of data and want to optimize some particular number (say, turning anonymized personal data into a prediction of yearly medical costs). The dataset here intrigued me because it’s about learning from and reconstructing graphs, which is a very different kind of problem. In this post, I’ll discuss my approach and insights on the problem.

Continue reading →

My Favorite Linux Command Line Tricks

July 28, 2014sdenton42 Comments

Dual Linux — My laptop, android phone, and a Raspberry Pi plugged into a crappy hotel TV, all running terminals. This happened while trying to compile Sage on the Pi in January, 2012.

This week I’m at the IMA workshop on Modern Applications of Representation Theory. So far it’s been really cool!

One of the graduate students asked me about how one goes about learning the Linux command line, so I thought I would write down a few of the things I think are most useful on a day-to-day basis. Such a list is sure to stir controversy, so feel free to comment if you see a grievous omission. In fact, I learned the command line mainly through installing Gentoo Linux back before there was any automation whatsoever in the process, and suffering through lengthy forum posts getting every bit of my system more-or-less working. (Note: Starting with Gentoo is probably a bad idea. I chose it at the time because it had the best forums, but there are probably better places to start these days. I mainly use Xubuntu these days.)

So, off to the races. I’m going to skip the really, really basic ones, like ls, cd, apt-get and sudo. In fact, there’s a nice tutorial at LinuxCommand.org which covers a lot of the basics, including IO redirection. Finally, I’m assuming that one is using the bash terminal.

Continue reading →

Winter on Georgian Bay

May 16, 2014May 16, 2014sdenton41 Comment

Back in late December, I planted a Raspberry Pi camera at a cottage on Georgian Bay, in Northern Ontario, set to take a picture once every two minutes. I had been planning the shoot for a couple months prior to the deployment: There were two Raspberry Pi’s involved, in case one failed somewhere during the winter. One of the Pi’s was set to reboot once a week, just in case the software crashed but the Pi was still awake. I had also written some software for the time-lapse to ensure that pictures were only taken during the day time, and to try to maintain a balance of well-lit, consistent images over the course of each day.

In spite of all the planning, I had a sense that something would go horribly wrong, and, indeed, when we showed up to the cottage, the windows were completely frosted over. The cameras had to be placed inside, so we figured we would mainly see the back-side of an icy window when we retrieved the cameras. Or that the camera boards would literally freeze after about a week of sub-zero temperatures in the unheated cottage. Or that a raccoon would find it way in and gnaw through the shiny Lego cases. Or something else entirely unplanned for.

So it was a bit of a surprise when it turned out that the shoot went perfectly. We retrieved the cameras about a week ago, on May 7th, and found over 42,000 photos waiting for us on one of the cameras and somewhat fewer on the other. Both cameras had survived the winter just fine!

All told, I think the result was really cool! The video at the top is the ‘highlights’ reel, with all of the best days. It comes to 13 minutes at 18 frames per second. Turns out it was a fantastic winter for doing a time-lapse, with lots of snow storms and ice. There’s even the occasional bit of wildlife, if you watch closely. I’ll post the full 40-minute time-lapse on Youtube sometime next week.

Continue reading →

One Weird Fourier Trick for Combinatorial Data

April 29, 2014April 29, 2014sdenton4

Cell phone photo from the scene of the crime

Here are the slides from the talk I gave in Montreal last Friday.

The talk was about using Fourier transforms to get polynomial-time encodings of permutation statistics, as well as a look at the Kondor-Borgwardt approach to graph invariants via the Fourier transform over $S_n$ . The talk was given at a representation theory conference, and I was making the point that we can get new research ideas by taking trips into the world of applications – in my case, by looking at machine learning problems. The opening joke was that I asked my computer for the best possible title for the talk, and received the click-bait title as a response. It was admittedly a pretty funny moment watching the chair of the session trying to decide whether to read the title originally submitted for the talk (‘Compressed Combinatorial Statistics’) or the ridiculousness on the screen (he went with the original).

Finding Community

February 12, 2014February 12, 2014sdenton4

I attended a really nice talk by Arash Amini yesterday about detecting ‘communities’ in sparse graphs. The basic problem is: In a big graph (like the Facebook graph, or the graph of scientific papers citations) you have clusters of friends/associates, and you want to pick out those clusters. Dr. Amini and his collaborators have been working on methods to solve this problem in particularly noisy cases. The methods presented were developed for cases where you know the specific number of clusters you are seeking to find. It was a fascinating talk, and I came away wondering if there are good methods to use when you aren’t sure of how many clusters there are.

Continue reading →

RoShamBo Part IV: Implementation

February 11, 2014February 11, 2014sdenton4

I’ve finally had a bit of time to finish up the code for the Rock-Paper-Scissors bot discussed in the previous posts; I’ve put the code in a GitHub repository here. Feel free to file issues if you would like it to be a bit more user friendly.

Win percentage over time, Diaconis vs Switchbot. As time increases, the win percentage settles in on 2/3's which is a natural limit for play against Switchbot. — Win percentage over time, Diaconis vs Switchbot. As time increases, the win percentage settles in on 2/3’s which is a natural limit for play against Switchbot.

The bot which uses the Fourier transform on move probabilities to search for profitable patterns is named `diaconis`, after Persi Diaconis. It’s currently working just fine, but is a bit slow computationally. On startup, it generates all possible move patterns that it will investigate during the course of each game, as well as some character tables. After each play, it tests some of these patterns, and tries to determine if their predictive power is better than any of the patterns seen thus far. If so, it begins using that pattern to choose move probabilities.

This works fine as a proof-of-concept of the basic ideas. Additional improvements could be had by doing some code optimization to speed things up a bit, and keeping a list of good patterns and allowing a bit more dexterity in switching between the patterns used for prediction.

Escape From the Box Factory: Better Single Variable Optimization Problems

January 31, 2014February 11, 2014sdenton41 Comment

I’m teaching an intro calculus class this year (specifically, ‘Math for Life and Social Science’), and came a while ago to the section on optimization. It’s a really important subject, and yet the optimization problems one finds in Calculus books (even good ones) tend to be contrived examples which I refer to as ‘box factory problems.’ Things along the lines of ‘minimize the surface area of a rectangular box with volume $1000 cm^3$ ‘.

Hey, kids! Let's take a field trip to the box factory! — Hey, kids! Let’s take a field trip to the box factory!

These are fine for a problem or two: There’s a useful skill in taking a real-sounding problem and translating it into the mathematics you’re learning. We use the constraints (in this case, on the volume) to reduce the number of dimensions, turn the problem into a one-variable calculus problem, and then solve. All well and good, but these problems somehow completely miss the impact of optimization on society at large. Largely because the optimization problems that occur most commonly in the wild have a slightly different flavour.

Problem: In Boston, we observe that the monthly rent for three one-bedroom apartments are $1300, $1150, and $950. Rent on three two-bedroom apartments were $1500, $1700, and $1200. Assuming that the cost of a 0-bedroom apartment is $500, find the best possible line describing the rent as a function of the number of bedrooms. Continue reading →

Roshambo Part III – Representation Theory

January 29, 2014February 11, 2014sdenton4

In the last two posts, we’ve looked at using machine learning for playing iterated Roshambo. Specifically, we saw how to use Bayes’ theorem to try to detect and exploit patterns, and then saw how Fourier transforms can give us a concrete measurement of the randomness (and non-randomness) in our opponent’s play. Today’s post is about how we can use representation theory to improve our chances of finding interesting patterns.

Niels Henrik Abel, for whom 'Abelian groups' are named. — Niels Henrik Abel, for whom ‘Abelian groups’ are named. These are groups where $xy=yx$ for any *x, y.*

Niels Henrik Abel, for whom ‘Abelian groups’ are named. These are groups where $xy=yx$ for any *x, y.*

Continue reading →